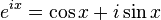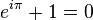原文地址
一、导言 对于大多数图形渲染开发者,GPU是既熟悉又陌生的部件,熟悉的是每天都需要跟它打交道,陌生的是GPU就如一个黑盒,不知道其内部硬件架构,更无从谈及其运行机制。
本文以NVIDIA作为主线,将试图全面且深入地剖析GPU的硬件架构及运行机制,主要涉及PC桌面级的GPU,不会覆盖移动端、专业计算、图形工作站级别的GPU。
若要通读本文,要求读者有一定图形学的基础,了解GPU渲染管线,最好写过HLSL、GLSL等shader代码。
1.1 为何要了解GPU? 了解GPU硬件架构和理解运行机制,笔者认为好处多多,总结出来有:
理解GPU其物理结构和运行机制,GPU由黑盒变白盒。 更易找出渲染瓶颈,写出高效率shader代码。 紧跟时代潮流,了解最前沿渲染技术! 技多不压身! 1.2 内容要点 本文的内容要点提炼如下:
GPU简介、历史、特性。 GPU硬件架构。 GPU和CPU的协调调度机制。 GPU缓存结构。 GPU渲染管线。 GPU运行机制。 GPU优化技巧。 1.3 带着问题阅读 适当带着问题去阅读技术文章,通常能加深理解和记忆,阅读本文可带着以下问题:
1、GPU是如何与CPU协调工作的?
2、GPU也有缓存机制吗?有几层?它们的速度差异多少?
3、GPU的渲染流程有哪些阶段?它们的功能分别是什么?
4、Early-Z技术是什么?发生在哪个阶段?这个阶段还会发生什么?会产生什么问题?如何解决?
5、SIMD和SIMT是什么?它们的好处是什么?co-issue呢?
6、GPU是并行处理的么?若是,硬件层是如何设计和实现的?
7、GPC、TPC、SM是什么?Warp又是什么?它们和Core、Thread之间的关系如何?
8、顶点着色器(VS)和像素着色器(PS)可以是同一处理单元吗?为什么?
9、像素着色器(PS)的最小处理单位是1像素吗?为什么?会带来什么影响?
10、Shader中的if、for等语句会降低渲染效率吗?为什么?
11、如下图,渲染相同面积的图形,三角形数量少(左)的还是数量多(右)的效率更快?为什么?
12、GPU Context是什么?有什么作用?
13、造成渲染瓶颈的问题很可能有哪些?该如何避免或优化它们?
如果阅读完本文,能够非常清晰地回答以上所有问题,那么,恭喜你掌握到本文的精髓了!
二、GPU概述 2.1 GPU是什么? GPU 全称是Graphics Processing Unit ,图形处理单元。它的功能最初与名字一致,是专门用于绘制图像和处理图元数据的特定芯片,后来渐渐加入了其它很多功能。
NVIDIA GPU芯片实物图 。
我们日常讨论GPU和显卡时,经常混为一谈,严格来说是有所区别的。GPU是显卡(Video card、Display card、Graphics card)最核心的部件,但除了GPU,显卡还有扇热器、通讯元件、与主板和显示器连接的各类插槽。
对于PC桌面,生产GPU的厂商主要有两家:
NVIDIA :英伟达,是当今首屈一指的图形渲染技术的引领者和GPU生产商佼佼者。NVIDIA的产品俗称N卡,代表产品有GeForce系列、GTX系列、RTX系列等。AMD :既是CPU生产商,也是GPU生产商,它家的显卡俗称A卡。代表产品有Radeon系列。 当然,NVIDIA和AMD也都生产移动端、图形工作站类型的GPU。此外,生产移动端显卡的厂商还有ARM、Imagination Technology、高通等公司。
2.2 GPU历史 GPU自从上世纪90年代出现雏形以来,经过20多年的发展,已经发展成不仅仅是渲染图形这么简单,还包含了数学计算、物理模拟、AI运算等功能。
2.2.1 NV GPU发展史 以下是GPU发展节点表:
NV1的渲染画面及其特性。 1997 – Riva 128 (NV3), DX3 1998 – Riva TNT (NV4), DX5 32位颜色, 24位Z缓存, 8位模板缓存 双纹理, 双线性过滤 每时钟2像素 (2 ppc) 1999 – GeForce 256(NV10) 固定管线 ,支持DirectX 7.0硬件T&L (Transform & lighting,坐标变换和光照)立方体环境图(Cubemaps) DOT3 – bump mapping 2倍各向异性过滤 三线性过滤 DXT纹理压缩 4ppc 引入“GPU”术语 NV10的渲染画面及其特性。 2001 – GeForce 3 DirectX 8.0 Shader Model 1.0 可编程渲染管线 3D纹理 硬件阴影图 8倍各向异性过滤 多采样抗锯齿(MSAA) 4 ppc NV20的渲染画面及其特性。 2003 – GeForce FX系列(NV3x) DirectX 9.0 Shader Model 2.0256顶点操作指令 32纹理 + 64算术像素操作指令 Shader Model 2.0a 着色语言 NV30的渲染画面及其特性。
2004 – GeForce 6系列 (NV4x) DirectX 9.0c Shader Model 3.0 动态流控制 顶点纹理读取 高动态范围(HDR)64位渲染纹理(Render Target) FP16*4 纹理过滤和混合 NV40的渲染画面及其特性。
2006 – GeForce 8系列 (G8x) DirectX 10.0 Shader Model 4.0几何着色器(Geometry Shaders) 没有上限位(No caps bits) 统一的着色器(Unified Shaders) Vista系统全新驱动 基于GPU计算的CUDA问世 GPU计算能力以GFLOPS计量。 NV G80的渲染画面及其特性。 2010 – GeForce 405(GF119) DirectX 11.0曲面细分(Tessellation) 外壳着色器(Hull Shader) 镶嵌单元(tessellator) 域着色器(Domain Shader) 计算着色器(Compute Shader) Vertex Shader. Hull Shader. Tessellator. Domain Shader. Stream Output. Geometry Shader. Rasterizer. Data Structure. Compute Shader. Pixel Shader. Output Merger. DirectX 11的渲染管线。 Shader Model 5.0 更多指令、存储单元、寄存器 面向对象着色语言 曲面细分 计算着色器 支持RTX光线追踪的显卡列表。 2018 – TITAN RTX(TU102) DirectX 12.1,OpenGL 4.5 6GPC,36TPC,72SM,72RT Core,… 8K分辨率,1770MHz主频,24G显存,384位带宽 从上面可以看出来,GPU硬件是伴随着图形API标准、游戏一起发展的,并且它们形成了相互相成、相互促进的良性关系。
2.2.2 NV GPU架构发展史 众所周知,CPU的发展符合摩尔定律:每18个月速度翻倍。
处理芯片晶体管数量符合摩尔定律,图右是摩尔本人,Intel的创始人
而NVIDIA创始人黄仁勋 在很多年前曾信誓旦旦地说,GPU的速度和功能要超越摩尔定律,每6个月就翻一倍。NV的GPU发展史证明,他确实做到了!GPU的提速幅率远超CPU:
NVIDIA GPU架构历经多次变革,从起初的Tesla发展到最新的Turing架构,发展史可分为以下时间节点:
2008 – Tesla Tesla最初是给计算处理单元使用的,应用于早期的CUDA系列显卡芯片中,并不是真正意义上的普通图形处理芯片。2010 – Fermi Fermi是第一个完整的GPU计算架构。首款可支持与共享存储结合纯cache层次的GPU架构,支持ECC的GPU架构。2012 – Kepler Kepler相较于Fermi更快,效率更高,性能更好。2014 – Maxwell 其全新的立体像素全局光照 (VXGI) 技术首次让游戏 GPU 能够提供实时的动态全局光照效果。基于 Maxwell 架构的 GTX 980 和 970 GPU 采用了包括多帧采样抗锯齿 (MFAA)、动态超级分辨率 (DSR)、VR Direct 以及超节能设计在内的一系列新技术。2016 – Pascal Pascal 架构将处理器和数据集成在同一个程序包内,以实现更高的计算效率。1080系列、1060系列基于Pascal架构2017 – Volta Volta 配备640 个Tensor 核心,每秒可提供超过100 兆次浮点运算(TFLOPS) 的深度学习效能,比前一代的Pascal 架构快5 倍以上。2018 – Turing Turing 架构配备了名为 RT Core 的专用光线追踪处理器,能够以高达每秒 10 Giga Rays 的速度对光线和声音在 3D 环境中的传播进行加速计算。Turing 架构将实时光线追踪运算加速至上一代 NVIDIA Pascal™ 架构的 25 倍,并能以高出 CPU 30 多倍的速度进行电影效果的最终帧渲染。2060系列、2080系列显卡也是跳过了Volta直接选择了Turing架构。下图是部分GPU架构的发展历程:
2.3 GPU的功能 现代GPU除了绘制图形外,还担当了很多额外的功能,综合起来如下几方面:
图形绘制。 这是GPU最传统的拿手好戏,也是最基础、最核心的功能。为大多数PC桌面、移动设备、图形工作站提供图形处理和绘制功能。物理模拟。 GPU硬件集成的物理引擎(PhysX、Havok),为游戏、电影、教育、科学模拟等领域提供了成百上千倍性能的物理模拟,使得以前需要长时间计算的物理模拟得以实时呈现。海量计算。 计算着色器及流输出的出现,为各种可以并行计算的海量需求得以实现,CUDA就是最好的例证。AI运算。 近年来,人工智能的崛起推动了GPU集成了AI Core运算单元,反哺AI运算能力的提升,给各行各业带来了计算能力的提升。其它计算。 音视频编解码、加解密、科学计算、离线渲染等等都离不开现代GPU的并行计算能力和海量吞吐能力。三、GPU物理架构 3.1 GPU宏观物理结构 由于纳米工艺的引入,GPU可以将数以亿记的晶体管和电子器件集成在一个小小的芯片内。从宏观物理结构上看,现代大多数桌面级GPU的大小跟数枚硬币同等大小,部分甚至比一枚硬币还小(下图)。
高通骁龙853显示芯片比硬币还小
当GPU结合散热风扇、PCI插槽、HDMI接口等部件之后,就组成了显卡(下图)。
显卡不能独立工作,需要装载在主板上,结合CPU、内存、显存、显示器等硬件设备,组成完整的PC机。
搭载了显卡的主板。
3.2 GPU微观物理结构 GPU的微观结构因不同厂商、不同架构都会有所差异,但核心部件、概念、以及运行机制大同小异。下面将展示部分架构的GPU微观物理结构。
3.2.1 NVidia Tesla架构 Tesla微观架构总览图如上。下面将阐述它的特性和概念:
拥有7组TPC(Texture/Processor Cluster,纹理处理簇) 每个TPC有两组SM(Stream Multiprocessor,流多处理器) 每个SM包含:6个SP(Streaming Processor,流处理器) 2个SFU(Special Function Unit,特殊函数单元) L1缓存、MT Issue(多线程指令获取)、C-Cache(常量缓存)、共享内存 除了TPC核心单元,还有与显存、CPU、系统内存交互的各种部件。 3.2.2 NVidia Fermi架构 Fermi架构如上图,它的特性如下:
拥有16个SM 每个SM:2个Warp(线程束) 两组共32个Core 16组加载存储单元(LD/ST) 4个特殊函数单元(SFU) 每个Warp:16个Core Warp编排器(Warp Scheduler) 分发单元(Dispatch Unit) 每个Core:1个FPU(浮点数单元) 1个ALU(逻辑运算单元) 3.2.3 NVidia Maxwell架构 采用了Maxwell的GM204,拥有4个GPC,每个GPC有4个SM,对比Tesla架构来说,在处理单元上有了很大的提升。
3.2.4 NVidia Kepler架构 Kepler除了在硬件有了提升,有了更多处理单元之外,还将SM升级到了SMX。SMX是改进的架构,支持动态创建渲染线程(下图),以降低延迟。
3.2.5 NVidia Turing架构 上图是采纳了Turing架构的TU102 GPU,它的特点如下:
6 GPC(图形处理簇) 36 TPC(纹理处理簇) 72 SM(流多处理器) 每个GPC有6个TPC,每个TPC有2个SM 4,608 CUDA核 72 RT核 576 Tensor核 288 纹理单元 12×32位 GDDR6内存控制器 (共384位) 单个SM的结构图如下:
每个SM包含:
64 CUDA核 8 Tensor核 256 KB寄存器文件 TU102 GPU芯片实物图:
3.3 GPU架构的共性 纵观上一节的所有GPU架构,可以发现它们虽然有所差异,但存在着很多相同的概念和部件:
GPC TPC Thread SM、SMX、SMM Warp SP Core ALU FPU SFU ROP Load/Store Unit L1 Cache L2 Cache Memory Register File 以上各个部件的用途将在下一章详细阐述。
GPU为什么会有这么多层级且有这么多雷同的部件?答案是GPU的任务是天然并行的,现代GPU的架构皆是以高度并行能力而设计的。
四、GPU运行机制 4.1 GPU渲染总览 由上一章可得知,现代GPU有着相似的结构,有很多相同的部件,在运行机制上,也有很多共同点。下面是Fermi架构的运行机制总览图:
从Fermi开始NVIDIA使用类似的原理架构,使用一个Giga Thread Engine来管理所有正在进行的工作,GPU被划分成多个GPCs(Graphics Processing Cluster),每个GPC拥有多个SM(SMX、SMM)和一个光栅化引擎(Raster Engine),它们其中有很多的连接,最显著的是Crossbar,它可以连接GPCs和其它功能性模块(例如ROP或其他子系统)。
程序员编写的shader是在SM上完成的。每个SM包含许多为线程执行数学运算的Core(核心)。例如,一个线程可以是顶点或像素着色器调用。这些Core和其它单元由Warp Scheduler驱动,Warp Scheduler管理一组32个线程作为Warp(线程束)并将要执行的指令移交给Dispatch Units。
GPU中实际有多少这些单元(每个GPC有多少个SM,多少个GPC ……)取决于芯片配置本身。例如,GM204有4个GPC,每个GPC有4个SM,但Tegra X1有1个GPC和2个SM,它们均采用Maxwell设计。SM设计本身(内核数量,指令单位,调度程序……)也随着时间的推移而发生变化,并帮助使芯片变得如此高效,可以从高端台式机扩展到笔记本电脑移动。
如上图,对于某些GPU(如Fermi部分型号)的单个SM,包含:
32个运算核心 (Core,也叫流处理器Stream Processor) 16个LD/ST(load/store)模块来加载和存储数据 4个SFU(Special function units)执行特殊数学运算(sin、cos、log等) 128KB寄存器(Register File) 64KB L1缓存 全局内存缓存(Uniform Cache) 纹理读取单元 纹理缓存(Texture Cache) PolyMorph Engine:多边形引擎负责属性装配(attribute Setup)、顶点拉取(VertexFetch)、曲面细分、栅格化(这个模块可以理解专门处理顶点相关的东西)。 2个Warp Schedulers:这个模块负责warp调度,一个warp由32个线程组成,warp调度器的指令通过Dispatch Units送到Core执行。 指令缓存(Instruction Cache) 内部链接网络(Interconnect Network) 4.2 GPU逻辑管线 了解上一节的部件和概念之后,可以深入阐述GPU的渲染过程和步骤。下面将以Fermi家族的SM为例,进行逻辑管线的详细说明。
1、程序通过图形API(DX、GL、WEBGL)发出drawcall指令,指令会被推送到驱动程序,驱动会检查指令的合法性,然后会把指令放到GPU可以读取的Pushbuffer中。
2、经过一段时间或者显式调用flush指令后,驱动程序把Pushbuffer的内容发送给GPU,GPU通过主机接口(Host Interface)接受这些命令,并通过前端(Front End)处理这些命令。
3、在图元分配器(Primitive Distributor)中开始工作分配,处理indexbuffer中的顶点产生三角形分成批次(batches),然后发送给多个PGCs。这一步的理解就是提交上来n个三角形,分配给这几个PGC同时处理。
4、在GPC中,每个SM中的Poly Morph Engine负责通过三角形索引(triangle indices)取出三角形的数据(vertex data),即图中的Vertex Fetch模块。
5、在获取数据之后,在SM中以32个线程为一组的线程束(Warp)来调度,来开始处理顶点数据。Warp是典型的单指令多线程(SIMT,SIMD单指令多数据的升级)的实现,也就是32个线程同时执行的指令是一模一样的,只是线程数据不一样,这样的好处就是一个warp只需要一个套逻辑对指令进行解码和执行就可以了,芯片可以做的更小更快,之所以可以这么做是由于GPU需要处理的任务是天然并行的。
6、SM的warp调度器会按照顺序分发指令给整个warp,单个warp中的线程会锁步(lock-step)执行各自的指令,如果线程碰到不激活执行的情况也会被遮掩(be masked out)。被遮掩的原因有很多,例如当前的指令是if(true)的分支,但是当前线程的数据的条件是false,或者循环的次数不一样(比如for循环次数n不是常量,或被break提前终止了但是别的还在走),因此在shader中的分支会显著增加时间消耗,在一个warp中的分支除非32个线程都走到if或者else里面,否则相当于所有的分支都走了一遍,线程不能独立执行指令而是以warp为单位,而这些warp之间才是独立的。
7、warp中的指令可以被一次完成,也可能经过多次调度,例如通常SM中的LD/ST(加载存取)单元数量明显少于基础数学操作单元。
8、由于某些指令比其他指令需要更长的时间才能完成,特别是内存加载,warp调度器可能会简单地切换到另一个没有内存等待的warp,这是GPU如何克服内存读取延迟的关键,只是简单地切换活动线程组。为了使这种切换非常快,调度器管理的所有warp在寄存器文件中都有自己的寄存器。这里就会有个矛盾产生,shader需要越多的寄存器,就会给warp留下越少的空间,就会产生越少的warp,这时候在碰到内存延迟的时候就会只是等待,而没有可以运行的warp可以切换。
9、一旦warp完成了vertex-shader的所有指令,运算结果会被Viewport Transform模块处理,三角形会被裁剪然后准备栅格化,GPU会使用L1和L2缓存来进行vertex-shader和pixel-shader的数据通信。
10、接下来这些三角形将被分割,再分配给多个GPC,三角形的范围决定着它将被分配到哪个光栅引擎(raster engines),每个raster engines覆盖了多个屏幕上的tile,这等于把三角形的渲染分配到多个tile上面。也就是像素阶段就把按三角形划分变成了按显示的像素划分了。
11、SM上的Attribute Setup保证了从vertex-shader来的数据经过插值后是pixel-shade是可读的。
12、GPC上的光栅引擎(raster engines)在它接收到的三角形上工作,来负责这些这些三角形的像素信息的生成(同时会处理裁剪Clipping、背面剔除和Early-Z剔除)。
13、32个像素线程将被分成一组,或者说8个2×2的像素块,这是在像素着色器上面的最小工作单元,在这个像素线程内,如果没有被三角形覆盖就会被遮掩,SM中的warp调度器会管理像素着色器的任务。
14、接下来的阶段就和vertex-shader中的逻辑步骤完全一样,但是变成了在像素着色器线程中执行。 由于不耗费任何性能可以获取一个像素内的值,导致锁步执行非常便利,所有的线程可以保证所有的指令可以在同一点。
15、最后一步,现在像素着色器已经完成了颜色的计算还有深度值的计算,在这个点上,我们必须考虑三角形的原始api顺序,然后才将数据移交给ROP(render output unit,渲染输入单元),一个ROP内部有很多ROP单元,在ROP单元中处理深度测试,和framebuffer的混合,深度和颜色的设置必须是原子操作,否则两个不同的三角形在同一个像素点就会有冲突和错误。
4.3 GPU技术要点 由于上一节主要阐述GPU内部的工作流程和机制,为了简洁性,省略了很多知识点和过程,本节将对它们做进一步补充说明。
4.3.1 SIMD和SIMT SIMD (Single Instruction Multiple Data)是单指令多数据,在GPU的ALU单元内,一条指令可以处理多维向量(一般是4D)的数据。比如,有以下shader指令:
float4 c = a + b; // a, b都是float4类型
对于没有SIMD的处理单元,需要4条指令将4个float数值相加,汇编伪代码如下:
ADD c.x, a.x, b.x
ADD c.y, a.y, b.y
ADD c.z, a.z, b.z
ADD c.w, a.w, b.w
但有了SIMD技术,只需一条指令即可处理完:
SIMD_ADD c, a, bSIMT (Single Instruction Multiple Threads,单指令多线程)是SIMD的升级版,可对GPU中单个SM中的多个Core同时处理同一指令,并且每个Core存取的数据可以是不同的。
SIMT_ADD c, a, b
上述指令会被同时送入在单个SM中被编组的所有Core中,同时执行运算,但a、b 、c的值可以不一样:
4.3.2 co-issue co-issue 是为了解决SIMD运算单元无法充分利用的问题。例如下图,由于float数量的不同,ALU利用率从100%依次下降为75%、50%、25%。
为了解决着色器在低维向量的利用率低的问题,可以通过合并1D与3D或2D与2D的指令。例如下图,DP3指令用了3D数据,ADD指令只有1D数据,co-issue会自动将它们合并,在同一个ALU只需一个指令周期即可执行完。
但是,对于向量运算单元(Vector ALU),如果其中一个变量既是操作数又是存储数的情况,无法启用co-issue技术:
于是标量指令着色器 (Scalar Instruction Shader)应运而生,它可以有效地组合任何向量,开启co-issue技术,充分发挥SIMD的优势。
4.3.3 if – else语句 如上图,SM中有8个ALU(Core),由于SIMD的特性,每个ALU的数据不一样,导致if-else语句在某些ALU中执行的是true分支(黄色),有些ALU执行的是false分支(灰蓝色),这样导致很多ALU的执行周期被浪费掉了(即masked out),拉长了整个执行周期。最坏的情况,同一个SM中只有1/8(8是同一个SM的线程数,不同架构的GPU有所不同)的利用率。
同样,for循环也会导致类似的情形,例如以下shader代码:
void func(int count, int breakNum)
{
for(int i=0; i<count; ++i)
{
if (i == breakNum)
break;
else
// do something
}
}
由于每个ALU的count不一样,加上有break分支,导致最快执行完shader的ALU可能是最慢的N分之一的时间,但由于SIMD的特性,最快的那个ALU依然要等待最慢的ALU执行完毕,才能接下一组指令的活!也就白白浪费了很多时间周期。
4.3.4 Early-Z 早期GPU的渲染管线的深度测试是在像素着色器之后才执行(下图),这样会造成很多本不可见的像素执行了耗性能的像素着色器计算。
后来,为了减少像素着色器的额外消耗,将深度测试提至像素着色器之前(下图),这就是Early-Z技术的由来。
Early-Z技术可以将很多无效的像素提前剔除,避免它们进入耗时严重的像素着色器。Early-Z剔除的最小单位不是1像素,而是像素块 (pixel quad,2×2个像素,详见[4.3.6 ](#4.3.6 像素块(pixel quad)))。
但是,以下情况会导致Early-Z失效:
开启Alpha Test :由于Alpha Test需要在像素着色器后面的Alpha Test阶段比较,所以无法在像素着色器之前就决定该像素是否被剔除。开启Alpha Blend :启用了Alpha混合的像素很多需要与frame buffer做混合,无法执行深度测试,也就无法利用Early-Z技术。开启Tex Kill :即在shader代码中有像素摒弃指令(DX的discard,OpenGL的clip)。关闭深度测试 。Early-Z是建立在深度测试看开启的条件下,如果关闭了深度测试,也就无法启用Early-Z技术。开启Multi-Sampling :多采样会影响周边像素,而Early-Z阶段无法得知周边像素是否被裁剪,故无法提前剔除。以及其它任何导致需要混合后面颜色的操作。 此外,Early-Z技术会导致一个问题:深度数据冲突 (depth data hazard)。
例子要结合上图,假设数值深度值5已经经过Early-Z即将写入Frame Buffer,而深度值10刚好处于Early-Z阶段,读取并对比当前缓存的深度值15,结果就是10通过了Early-Z测试,会覆盖掉比自己小的深度值5,最终frame buffer的深度值是错误的结果。
避免深度数据冲突的方法之一是在写入深度值之前,再次与frame buffer的值进行对比:
4.3.5 统一着色器架构(Unified shader Architecture) 在早期的GPU,顶点着色器和像素着色器的硬件结构是独立的,它们各有各的寄存器、运算单元等部件。这样很多时候,会造成顶点着色器与像素着色器之间任务的不平衡。对于顶点数量多的任务,像素着色器空闲状态多;对于像素多的任务,顶点着色器的空闲状态多(下图)。
于是,为了解决VS和PS之间的不平衡,引入了统一着色器架构(Unified shader Architecture)。用了此架构的GPU,VS和PS用的都是相同的Core。也就是,同一个Core既可以是VS又可以是PS。
这样就解决了不同类型着色器之间的不平衡问题,还可以减少GPU的硬件单元,压缩物理尺寸和耗电量。此外,VS、PS可还可以和其它着色器(几何、曲面、计算)统一为一体。
4.3.6 像素块(Pixel Quad) 上一节步骤13提到:
32个像素线程将被分成一组,或者说8个2×2的像素块 ,这是在像素着色器上面的最小工作单元 ,在这个像素线程内,如果没有被三角形覆盖就会被遮掩,SM中的warp调度器会管理像素着色器的任务。
也就是说,在像素着色器中,会将相邻的四个像素作为不可分隔的一组,送入同一个SM内4个不同的Core。
为什么像素着色器处理的最小单元是2×2的像素块?
笔者推测有以下原因:
1、简化和加速像素分派的工作。
2、精简SM的架构,减少硬件单元数量和尺寸。
3、降低功耗,提高效能比。
4、无效像素虽然不会被存储结果,但可辅助有效像素求导函数。详见4.6 利用扩展例证 。
这种设计虽然有其优势,但同时,也会激化过绘制(Over Draw)的情况,损耗额外的性能。比如下图中,白色的三角形只占用了3个像素(绿色),按我们普通的思维,只需要3个Core绘制3次就可以了。
但是,由于上面的3个像素分别占据了不同的像素块(橙色分隔),实际上需要占用12个Core绘制12次(下图)。
这就会额外消耗300%的硬件性能,导致了更加严重的过绘制情况。
更多详情可以观看虚幻官方的视频教学:实时渲染深入探究 。
4.4 GPU资源机制 本节将阐述GPU的内存访问、资源管理等机制。
4.4.1 内存架构 部分架构的GPU与CPU类似,也有多级缓存结构:寄存器、L1缓存、L2缓存、GPU显存、系统显存。
它们的存取速度从寄存器到系统内存依次变慢:
存储类型 寄存器 共享内存 L1缓存 L2缓存 纹理、常量缓存 全局内存 访问周期 1 1~32 1~32 32~64 400~600 400~600
由此可见,shader直接访问寄存器、L1、L2缓存还是比较快的,但访问纹理、常量缓存和全局内存非常慢,会造成很高的延迟。
上面的多级缓存结构可被称为“CPU-Style”,还存在GPU-Style的内存架构:
这种架构的特点是ALU多,GPU上下文(Context)多,吞吐量高,依赖高带宽与系统内存交换数据。
4.4.2 GPU Context和延迟 由于SIMT技术的引入,导致很多同一个SM内的很多Core并不是独立的,当它们当中有部分Core需要访问到纹理、常量缓存和全局内存时,就会导致非常大的卡顿(Stall)。
例如下图中,有4组上下文(Context),它们共用同一组运算单元ALU。
假设第一组Context需要访问缓存或内存,会导致2~3个周期的延迟,此时调度器会激活第二组Context以利用ALU:
当第二组Context访问缓存或内存又卡住,会依次激活第三、第四组Context,直到第一组Context恢复运行或所有都被激活:
延迟的后果是每组Context的总体执行时间被拉长了:
但是,越多Context可用就越可以提升运算单元的吞吐量,比如下图的18组Context的架构可以最大化地提升吞吐量:
4.4.3 CPU-GPU异构系统 根据CPU和GPU是否共享内存,可分为两种类型的CPU-GPU架构:
上图左是分离式架构 ,CPU和GPU各自有独立的缓存和内存,它们通过PCI-e等总线通讯。这种结构的缺点在于 PCI-e 相对于两者具有低带宽和高延迟,数据的传输成了其中的性能瓶颈。目前使用非常广泛,如PC、智能手机等。
上图右是耦合式架构 ,CPU 和 GPU 共享内存和缓存。AMD 的 APU 采用的就是这种结构,目前主要使用在游戏主机中,如 PS4。
在存储管理方面,分离式结构中 CPU 和 GPU 各自拥有独立的内存,两者共享一套虚拟地址空间,必要时会进行内存拷贝。对于耦合式结构,GPU 没有独立的内存,与 GPU 共享系统内存,由 MMU 进行存储管理。
4.4.4 GPU资源管理模型 下图是分离式架构的资源管理模型:
MMIO(Memory Mapped IO) CPU与GPU的交流就是通过MMIO进行的。CPU 通过 MMIO 访问 GPU 的寄存器状态。 DMA传输大量的数据就是通过MMIO进行命令控制的。 I/O端口可用于间接访问MMIO区域,像Nouveau等开源软件从来不访问它。 GPU Context GPU Context代表了GPU计算的状态。 在GPU中拥有自己的虚拟地址。 GPU 中可以并存多个活跃态下的Context。 GPU Channel 任何命令都是由CPU发出。 命令流(command stream)被提交到硬件单元,也就是GPU Channel。 每个GPU Channel关联一个context,而一个GPU Context可以有多个GPU channel。 每个GPU Context 包含相关channel的 GPU Channel Descriptors , 每个 Descriptor 都是 GPU 内存中的一个对象。 每个 GPU Channel Descriptor 存储了 Channel 的设置,其中就包括 Page Table 。 每个 GPU Channel 在GPU内存中分配了唯一的命令缓存,这通过MMIO对CPU可见。 GPU Context Switching 和命令执行都在GPU硬件内部调度。 GPU Page Table GPU Context在虚拟基地空间由Page Table隔离其它的Context 。 GPU Page Table隔离CPU Page Table,位于GPU内存中。 GPU Page Table的物理地址位于 GPU Channel Descriptor中。 GPU Page Table不仅仅将 GPU虚拟地址转换成GPU内存的物理地址,也可以转换成CPU的物理地址。因此,GPU Page Table可以将GPU虚拟地址和CPU内存地址统一到GPU统一虚拟地址空间来。 PCI-e BAR GPU 设备通过PCI-e总线接入到主机上。 Base Address Registers(BARs) 是 MMIO的窗口,在GPU启动时候配置。 GPU的控制寄存器和内存都映射到了BARs中。 GPU设备内存通过映射的MMIO窗口去配置GPU和访问GPU内存。 PFIFO Engine PFIFO是GPU命令提交通过的一个特殊的部件。 PFIFO维护了一些独立命令队列,也就是Channel。 此命令队列是Ring Buffer,有PUT和GET的指针。 所有访问Channel控制区域的执行指令都被PFIFO 拦截下来。 GPU驱动使用Channel Descriptor来存储相关的Channel设定。 PFIFO将读取的命令转交给PGRAPH Engine。 BO Buffer Object (BO),内存的一块(Block),能够用于存储纹理(Texture)、渲染目标(Render Target)、着色代码(shader code)等等。 Nouveau和Gdev经常使用BO。Nouveau是一个自由及开放源代码显卡驱动程序,是为NVidia的显卡所编写。Gdev是一套丰富的开源软件,用于NVIDIA的GPGPU技术,包括设备驱动程序。 更多详细可以阅读论文:Data Transfer Matters for GPU Computing 。
4.4.5 CPU-GPU数据流 下图是分离式架构的CPU-GPU的数据流程图:
1、将主存的处理数据复制到显存中。
2、CPU指令驱动GPU。
3、GPU中的每个运算单元并行处理。此步会从显存存取数据。
4、GPU将显存结果传回主存。
4.4.6 显像机制 水平和垂直同步信号 在早期的CRT显示器,电子枪从上到下逐行扫描,扫描完成后显示器就呈现一帧画面。然后电子枪回到初始位置进行下一次扫描。为了同步显示器的显示过程和系统的视频控制器,显示器会用硬件时钟产生一系列的定时信号。当电子枪换行进行扫描时,显示器会发出一个水平同步信号(horizonal synchronization),简称 HSync
当一帧画面绘制完成后,电子枪回复到原位,准备画下一帧前,显示器会发出一个垂直同步信号(vertical synchronization),简称 VSync 。
显示器通常以固定频率进行刷新,这个刷新率就是 VSync 信号产生的频率。虽然现在的显示器基本都是液晶显示屏了,但其原理基本一致。
CPU将计算好显示内容提交至 GPU,GPU 渲染完成后将渲染结果存入帧缓冲区,视频控制器会按照 VSync 信号逐帧读取帧缓冲区的数据,经过数据转换后最终由显示器进行显示。
双缓冲
在单缓冲下,帧缓冲区的读取和刷新都都会有比较大的效率问题,经常会出现相互等待的情况,导致帧率下降。
为了解决效率问题,GPU 通常会引入两个缓冲区,即 双缓冲机制 。在这种情况下,GPU 会预先渲染一帧放入一个缓冲区中,用于视频控制器的读取。当下一帧渲染完毕后,GPU 会直接把视频控制器的指针指向第二个缓冲器。
垂直同步
双缓冲虽然能解决效率问题,但会引入一个新的问题。当视频控制器还未读取完成时,即屏幕内容刚显示一半时,GPU 将新的一帧内容提交到帧缓冲区并把两个缓冲区进行交换后,视频控制器就会把新的一帧数据的下半段显示到屏幕上,造成画面撕裂现象:
为了解决这个问题,GPU 通常有一个机制叫做垂直同步 (简写也是V-Sync),当开启垂直同步后,GPU 会等待显示器的 VSync 信号发出后,才进行新的一帧渲染和缓冲区更新。这样能解决画面撕裂现象,也增加了画面流畅度,但需要消费更多的计算资源,也会带来部分延迟。 4.5 Shader运行机制 Shader代码也跟传统的C++等语言类似,需要将面向人类的高级语言(GLSL、HLSL、CGSL)通过编译器转成面向机器的二进制指令,二进制指令可转译成汇编代码,以便技术人员查阅和调试。
由高级语言编译成汇编指令的过程通常是在离线阶段执行,以减轻运行时的消耗。
在执行阶段,CPU端将shader二进制指令经由PCI-e推送到GPU端,GPU在执行代码时,会用Context将指令分成若干Channel推送到各个Core的存储空间。
对现代GPU而言,可编程的阶段越来越多,包含但不限于:顶点着色器(Vertex Shader)、曲面细分控制着色器(Tessellation Control Shader)、几何着色器(Geometry Shader)、像素/片元着色器(Fragment Shader)、计算着色器(Compute Shader)、…
这些着色器形成流水线式的并行化的渲染管线。下面将配合具体的例子说明。
下段是计算漫反射的经典代码:
sampler mySamp;
Texture2D<float3> myTex;
float3 lightDir;
float4 diffuseShader(float3 norm, float2 uv)
{
float3 kd;
kd = myTex.Sample(mySamp, uv);
kd *= clamp( dot(lightDir, norm), 0.0, 1.0);
return float4(kd, 1.0);
}
经过编译后成为汇编代码:
<diffuseShader>:
sample r0, v4, t0, s0
mul r3, v0, cb0[0]
madd r3, v1, cb0[1], r3
madd r3, v2, cb0[2], r3
clmp r3, r3, l(0.0), l(1.0)
mul o0, r0, r3
mul o1, r1, r3
mul o2, r2, r3
mov o3, l(1.0)
在执行阶段,以上汇编代码会被GPU推送到执行上下文(Execution Context),然后ALU会逐条获取(Detch)、解码(Decode)汇编指令,并执行它们。
以上示例图只是单个ALU的执行情况,实际上,GPU有几十甚至上百个执行单元在同时执行shader指令:
对于SIMT架构的GPU,汇编指令有所不同,变成了SIMT特定指令代码:
<VEC8_diffuseShader>:
VEC8_sample vec_r0, vec_v4, t0, vec_s0
VEC8_mul vec_r3, vec_v0, cb0[0]
VEC8_madd vec_r3, vec_v1, cb0[1], vec_r3
VEC8_madd vec_r3, vec_v2, cb0[2], vec_r3
VEC8_clmp vec_r3, vec_r3, l(0.0), l(1.0)
VEC8_mul vec_o0, vec_r0, vec_r3
VEC8_mul vec_o1, vec_r1, vec_r3
VEC8_mul vec_o2, vec_r2, vec_r3
VEC8_mov o3, l(1.0)
并且Context以Core为单位组成共享的结构,同一个Core的多个ALU共享一组Context:
如果有多个Core,就会有更多的ALU同时参与shader计算,每个Core执行的数据是不一样的,可能是顶点、图元、像素等任何数据:
4.6 利用扩展例证 NV shader thread group 提供了OpenGL的扩展,可以查询GPU线程、Core、SM、Warp等硬件相关的属性。如果要开启次此扩展,需要满足以下条件:
OpenGL 4.3+; GLSL 4.3+; 支持OpenGL 4.3+的NV显卡; 并且此扩展只在NV部分5代着色器内起作用:
This extension interacts with NV_gpu_program5
下面是具体的字段和代表的意义:
// 开启扩展
#extension GL_NV_shader_thread_group : require (or enable)
WARP_SIZE_NV // 单个线程束的线程数量
WARPS_PER_SM_NV // 单个SM的线程束数量
SM_COUNT_NV // SM数量
uniform uint gl_WarpSizeNV; // 单个线程束的线程数量
uniform uint gl_WarpsPerSMNV; // 单个SM的线程束数量
uniform uint gl_SMCountNV; // SM数量
in uint gl_WarpIDNV; // 当前线程束id
in uint gl_SMIDNV; // 当前线程束所在的SM id,取值[0, gl_SMCountNV-1]
in uint gl_ThreadInWarpNV; // 当前线程id,取值[0, gl_WarpSizeNV-1]
in uint gl_ThreadEqMaskNV; // 是否等于当前线程id的位域掩码。
in uint gl_ThreadGeMaskNV; // 是否大于等于当前线程id的位域掩码。
in uint gl_ThreadGtMaskNV; // 是否大于当前线程id的位域掩码。
in uint gl_ThreadLeMaskNV; // 是否小于等于当前线程id的位域掩码。
in uint gl_ThreadLtMaskNV; // 是否小于当前线程id的位域掩码。
in bool gl_HelperThreadNV; // 当前线程是否协助型线程。
上述所说的协助型线程gl_HelperThreadNV是指在处理2×2的像素块时,那些未被图元覆盖的像素着色器线程将被标记为gl_HelperThreadNV = true,它们的结果将被忽略,也不会被存储,但可辅助一些计算,如导数dFdx和dFdy。为了防止理解有误,贴出原文:
The variable gl_HelperThreadNV specifies if the current thread is a helper thread. In implementations supporting this extension, fragment shader invocations may be arranged in SIMD thread groups of 2×2 fragments called “quad”. When a fragment shader instruction is executed on a quad, it’s possible that some fragments within the quad will execute the instruction even if they are not covered by the primitive. Those threads are called helper threads. Their outputs will be discarded and they will not execute global store functions, but the intermediate values they compute can still be used by thread group sharing functions or by fragment derivative functions like dFdx and dFdy.
利用以上字段,可以编写特殊shader代码转成颜色信息,以便可视化窥探GPU的工作机制和流程。
利用NV扩展字段,可视化了顶点着色器、像素着色器的SM、Warp id,为我们查探GPU的工作机制和流程提供了途径。
下面正式进入验证阶段,将以Geforce RTX 2060作为验证对象,具体信息如下:
操作系统: Windows 10 Pro, 64-bit
DirectX 版本: 12.0
CUDA 核心: 1920
首先在应用程序创建包含两个三角形的顶点数据:
// set up vertex data (and buffer(s)) and configure vertex attributes
const float HalfSize = 1.0f;
float vertices[] = {
-HalfSize, -HalfSize, 0.0f, // left bottom
HalfSize, -HalfSize, 0.0f, // right bottom
-HalfSize, HalfSize, 0.0f, // top left
-HalfSize, HalfSize, 0.0f, // top left
HalfSize, -HalfSize, 0.0f, // right bottom
HalfSize, HalfSize, 0.0f, // top right
};
渲染采用的顶点着色器非常简单:
#version 430 core
layout (location = 0) in vec3 aPos;
void main()
{
gl_Position = vec4(aPos, 1.0f);
}
片元着色器也是寥寥数行:
#version 430 core
out vec4 FragColor;
void main()
{
FragColor = vec4(1.0f, 0.5f, 0.2f, 1.0f);
}
绘制出来的原始画面如下:
紧接着,修改片元着色器,加入扩展所需的代码,并修改颜色计算:
#version 430 core
#extension GL_NV_shader_thread_group : require
uniform uint gl_WarpSizeNV; // 单个线程束的线程数量
uniform uint gl_WarpsPerSMNV; // 单个SM的线程束数量
uniform uint gl_SMCountNV; // SM数量
in uint gl_WarpIDNV; // 当前线程束id
in uint gl_SMIDNV; // 当前线程所在的SM id,取值[0, gl_SMCountNV-1]
in uint gl_ThreadInWarpNV; // 当前线程id,取值[0, gl_WarpSizeNV-1]
out vec4 FragColor;
void main()
{
// SM id
float lightness = gl_SMIDNV / gl_SMCountNV;
FragColor = vec4(lightness);
}
由上面的代码渲染的画面如下:
从上面可分析出一些信息:
画面共有32个亮度色阶,也就是Geforce RTX 2060有32个SM。 单个SM每次渲染16×16为单位的像素块,也就是每个SM有256个Core。 SM之间不是顺序分配像素块,而是无序分配。 不同三角形的接缝处出现断层,说明同一个像素块如果分属不同的三角形,就会分配到不同的SM进行处理。由此推断,相同面积的区域,如果所属的三角形越多,就会导致分配给SM的次数越多,消耗的渲染性能也越多 。 接着修改片元着色器的颜色计算代码以显示Warp id:
// warp id
float lightness = gl_WarpIDNV / gl_WarpsPerSMNV;
FragColor = vec4(lightness);
得到如下画面:
由此可得出一些信息或推论:
画面共有32个亮度色阶,也就是每个SM有32个Warp,每个Warp有8个Core。 每个色块像素是4×8,由于每个Warp有8个Core,由此推断每个Core单次要处理2×2的最小单元像素块。 也是无序分配像素块。 三角形接缝处出现断层,同SM的推断一致。 再修改片元着色器的颜色计算代码以显示线程id:
// thread id
float lightness = gl_ThreadInWarpNV / gl_WarpSizeNV;
FragColor = vec4(lightness);
得到如下画面:
为了方便分析,用Photoshop对中间局部放大10倍,得到以下画面:
结合上面两幅图,也可以得出一些结论:
相较SM、线程束,线程分布图比较规律。说明同一个Warp的线程分布是规律的。 三角形接缝处出现紊乱,说明是不同的Warp造成了不同的线程。 画面有32个色阶,说明单个Warp有32个线程。 每个像素独占一个亮度色阶,与周边相邻像素都不同,说明每个线程只处理一个像素。 再次说明,以上画面和结论是基于Geforce RTX 2060,不同型号的GPU可能会不一样,得到的结果和推论也会有所不同。
更多NV扩展可参见OpenGL官网:NV extensions 。
五、总结 5.1 CPU vs GPU CPU和GPU的差异可以描述在下面表格中:
CPU GPU 延迟容忍度 低 高 并行目标 任务(Task) 数据(Data) 核心架构 多线程核心 SIMT核心 线程数量级别 10 10000 吞吐量 低 高 缓存需求量 高 低 线程独立性 低 高
它们之间的差异(缓存、核心数量、内存、线程数等)可用下图展示出来:
5.2 渲染优化建议 由上章的分析,可以很容易给出渲染优化建议:
减少CPU和GPU的数据交换: 合批(Batch) 减少顶点数、三角形数 视锥裁剪 避免每帧提交Buffer数据CPU版的粒子、动画会每帧修改、提交数据,可移至GPU端。 减少渲染状态设置和查询例如:glGetUniformLocation会从GPU内存查询状态,耗费很多时间周期。 避免每帧设置、查询渲染状态,可在初始化时缓存状态。 启用GPU Instance 开启LOD 避免从显存读数据 减少过绘制: 避免Tex Kill操作 避免Alpha Test 避免Alpha Blend 开启深度测试Early-Z 层次Z缓冲(Hierarchical Z-Buffering,HZB) 开启裁剪:背面裁剪 遮挡裁剪 视口裁剪 剪切矩形(scissor rectangle) 控制物体数量粒子数量多且面积小,由于像素块机制,会加剧过绘制情况 植物、沙石、毛发等也如此 Shader优化: 避免if、switch分支语句 避免for循环语句,特别是循环次数可变的 减少纹理采样次数 禁用clip或discard操作 减少复杂数学函数调用 更多优化技巧可阅读:
5.3 GPU的未来 从章节[2.2 GPU历史](#2.2 GPU历史)可以得出一些结论,也可以推测GPU发展的趋势:
硬件升级 。更多运算单元,更多存储空间,更高并发,更高带宽,更低延时。。。Tile-Based Rendering的集成 。基于瓦片的渲染可以一定程度降低带宽和提升光照计算效率,目前部分移动端及桌面的GPU已经引入这个技术,未来将有望成为常态。3D内存技术 。目前大多数传统的内存是2D的,3D内存则不同,在物理结构上是3D的,类似立方体结构,集成于芯片内。可获得几倍的访问速度和效能比。 GPU愈加可编程化 。GPU天生是并行且相对固定的,未来将会开放越来越多的shader可供编程,而CPU刚好相反,将往并行化发展。也就是说,未来的GPU越来越像CPU,而CPU越来越像GPU。难道它们应验了古语:合久必分,分久必合么? 实时光照追踪的普及 。基于Turing架构的GPU已经加入大量RT Core、HVB、AI降噪等技术,Hybrid Rendering Pipeline 就是此架构的光线追踪渲染管线,能够同时结合光栅化器、RT Core、Compute Core执行混合渲染: Hybrid Rendering Pipeline相当于光线追踪渲染管线和光栅化渲染管线的合体:
数据并发提升、深度神经网络、GPU计算单元等普及及提升 。 AI降噪和AI抗锯齿 。AI降噪已经在部分RTX系列的光线追踪版本得到应用,而AI抗锯齿(Super Res)可用于超高分辨率的视频图像抗锯齿: 基于任务和网格着色器的渲染管线 。基于任务和网格着色器的渲染管线(Graphics Pipeline with Task and Mesh Shaders)与传统的光栅化渲染光线有着很大的差异,它以线程组(Thread Group)、任务着色器(Task shader)和网格着色器(Mesh shader)为基础,形成一种全新的渲染管线: 5.4 结语 本文系统地讲解了GPU的历史、发展、工作流程,以及部分过程的细化说明和用到的各种技术,我们从中可以看到GPU架构的动机、机制、瓶颈,以及未来的发展。
希望看完本文,大家能很好地回答导言提出的问题:1.3 带着问题阅读 。如果不能全部回答,也没关系,回头看相关章节,总能找到答案。
如果想更深入地了解GPU的设计细节、实现细节,可阅读GPU厂商定期发布的白皮书和各大高校、机构发布的论文。推荐一个GPU解说视频:A trip through the Graphics Pipeline 2011: Index ,虽然是多年前的视频,但比较系统、全面地讲解了GPU的机制和技术。
特别说明 感谢所有参考文献的作者们! 原创文章,未经许可,禁止转载! 参考文献