pbrt是一个基于物理渲染的开源离线渲染器;
《Physically Based Rendering: From Theory to Implemention 3rd》是一本介绍pbr原理和pbrt的书;
系列文章是这本书各个章节的简单翻译,除此之外,对于书里一些没有深入阐述的内容,这里也会简单介绍。
书中前五章属于基础内容,不包含在系列文章内。第5章介绍了颜色的三种描述:光谱能量分布,XYZ和RGB。pbrt实现了这几种描述的转换(详细见Spectrum类),当我们提到一种颜色描述时,等价于其他两种描述。
pbrt渲染循环
pbrt基于光线追踪技术,因而定义一条射线与场景中的对象进行相交测试是必要的:
class Ray
{
Point3f o;
Vector3f d;
}pbrt使用Ray表示一条射线,由起始点o,和方向d定义。对于正交投影,起始点位于像素点,方向指向z轴正方向(pbrt使用左手坐标系);对于透视投影,起始点位于摄像机原点,也就是(0,0,0),方向指向像素点。
射线与场景中的几何物体进行相交测试,相交信息保存在SurfaceInteraction:
class SurfaceInteraction
{
Point3f p;
Normal3f n;
Point2f uv;
const Shape *shape = nullptr;
}保存了相交点坐标p, 法向量n,uv坐标,以及相交对象的指针shape.
对于二次曲面,uv坐标可以通过简单的数学计算得到,如特殊的二次曲面——球面,相交点的坐标可以转化为球面坐标(θ, φ)(θ∈[0, π], φ∈[0, 2π]),该坐标又可以转化为0到1范围内的(u, v)坐标:u = φ / 2π,v = θ / π。pbrt也给出了其他二次曲面uv坐标的计算。
对于三角面,uv坐标可能由建模工具提供,这时候,uv坐标由定义在三角形三个顶点的值插值得到。
相交点的几何法向量由相交位置p关于uv坐标的两个偏导数的叉积得到:∂p/∂u x ∂p/∂v.
同样pbrt也提供了这些偏导数的计算。
得到一个相交信息,可以确定该相交点应该着色:相交点与场景中的光源进行相交测试,判断其是否处于光照下,由反射模型(BRDF、BTDF和BSSRDF,以下简称为BxDF)确定反射多少光,pbrt的材质确定表面使用哪些反射模型,纹理则提供表面的外观属性,如漫反射颜色、粗糙度等。最终,沿着原始射线的相反方向返回到摄像机的光,在传播过程可能被场景中的烟、雾吸收或增强,这个过程由体积散射处理。由于采样不完全和高频信息的存在,最后得到的图像总是会存在走样,采样和重构技术尽可能减少走样(反走样)。
以上简单概括了pbrt在一个渲染循环里的主要工作内容。
光传导公式
这里有必要提一下书中第一章就介绍的光传导公式1.1(light transport equation):
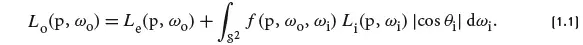
光线追踪技术之所以难以应用于实时渲染,很大程度上是因为其需要大量的计算(pbrt渲染一个简单场景就需要10多分钟),但渲染的图像也因此更接近真实场景:在真实场景中,对于上面相交测试得到的相交点p,接收的光不只来自光源,同时也可能来自其它非光源物体反射的光,光传导公式的积分就是计算来自所有方向的入射光Li反射回摄像机的光(使用BxDF模型确定反射多少光,即式中的函数f)的总和,再加上物体的自发光Le(如果自身是光源),得到返回摄像机的光能总和Lo。其中wo是返回摄像机的方向,wi为入射光方向,θi为wi与法向量的夹角(wi方向指向光源)。
事实上,要计算上面的积分是不可能的(这里面还涉及递归的光线追踪),但是仅选用一部分数量的入射光来接近真实场景渲染是可行的,例如,仅计算来自光源和沿着完全镜面反射和折射方向的入射光。pbrt的主要任务就是计算光传导公式1.1里的积分。
下面是之后几篇文章要介绍的内容:摄像机建模、采样和重构、反射模型、材质、纹理、体积散射。
相关资源:
pbrt源码:https://github.com/mmp/pbrt-v3
